場解算器

場求解器是積體電路設計人員和印刷電路板設計人員分析和最佳化其設計的電氣效能的重要工具。

什麼是場求解器？

場求解器是求解麥克斯韋方程組的電磁模擬軟體。它可以求解完整的麥克斯韋方程組（全波求解器），也可以求解部分集合，例如寄生電容或電感擷取。

電磁模擬軟體有助於模擬電磁場並求解複雜的方程，以確保最終產品的功能和可靠性。場求解器的一個常見區別是微分求解器和積分求解器，每種求解器都有自己的優點和應用。

了解好處

與使用標準寄生擷取工具相比，使用場求解器有哪些優點？

增強電路效能

獲得無與倫比的寄生電容運算精度，確保積體電路的最佳效能和可靠性。

提高設計效率

在設計過程的早期快速識別並解決潛在問題，從而顯著減少開發時間和成本。

確保產品完整性

透過準確模擬電磁相互作用，確保您的設計在各種操作條件下的完整性和功能性。

微分場求解器

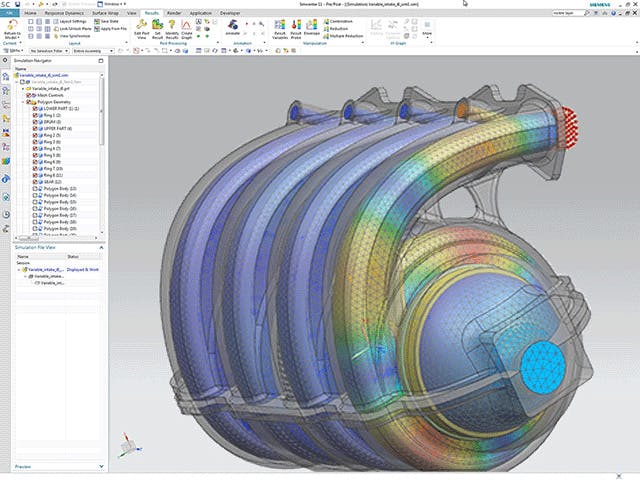
微分場求解器透過使用有限差分方法求解麥克斯韋方程組來運作。這些方法將空間離散成直線網格，計算每個點的電場和磁場。這種方法非常適合分析設計中的高頻效應和急劇轉變，例如印刷電路板上的訊號跡線或晶片上的互連。微分解算器的精確度取決於用於離散空間的網格單元的大小 - 較小的單元會導致更準確的結果，但需要更多的計算資源。

有限差分 (FD) 和有限元素 (FEM) 方法

該場的微分形式有兩種不同的形式：有限差分 (FD) 和有限元素 (FEM) 方法。有限差分法具有優異的收斂特性。透過適當調整網格解析度和數值方案，設計人員可以用最少的計算量獲得高精度的場方程式解。這使得它成為積體電路設計中時間關鍵型應用的有吸引力的選擇，因為快速週轉時間至關重要。

積分場求解器

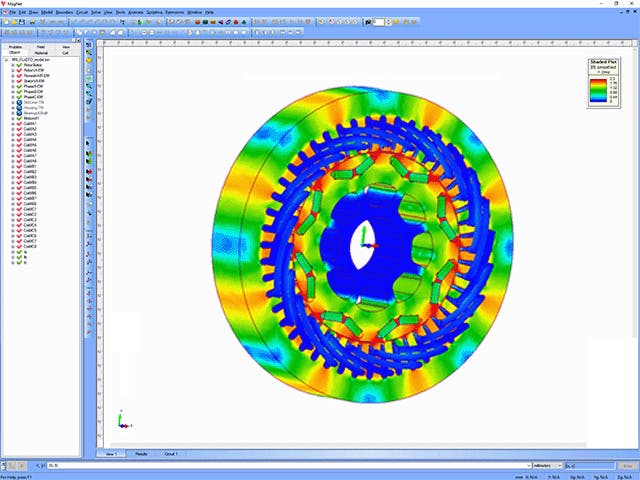
另一方面，積分場求解器使用數值積分技術來求解設計中表面或體積上的麥克斯韋方程式。積分求解器依靠電磁場源的離散化（例如表面電荷密度）來求解電容。常見的演算法包括邊界元法（BEM）和矩量法（MoM）。

浮動隨機遊走 (FRW) 求解器

浮動隨機遊走 (FRW) 演算法通常也與場求解器分組，但它們不是正式的場求解器，因為它們通常不會求解場。與使用確定性方法求解方程式的傳統場求解器不同，FRW 演算法透過將隨機遊走納入模擬中來引入隨機元素。這種隨機性可以更真實地表示複雜環境中的粒子運動。FRW 的主要缺點之一是演算法的耗時性。它需要大量迭代才能獲得準確的結果，這會顯著增加模擬時間。

Three differential integral floating solvers

由左至右：微分場求解器、積分場求解器和浮動隨機遊走的表示。使用微分場求解器（有限差分法 FDM 和有限元素法 FEM），晶片以直線網格表示。使用積分場求解器（邊界元法 BEM 和矩量法 MoM），僅對邊界進行離散化。使用浮動隨機遊走（它不是正式的場解算器，因為它不解場），可以模擬兩個導體之間粒子的隨機路徑。